Strontium sorption on hematite at elevated temperatures
Olga N.Karasyova, Lyudmila I.Ivanova, Leonid Z.Lakshtanov
Institute of Experimental Mineralogy of Russian Academy of Sciences,
142432 Chernogolovka, Moscow district, Russia
and
Lars Lövgren
Department of Inorganic Chemistry, University of Umeå,
S-901 87 Umeå, Sweden
Introduction
Adsorption on the mineral surfaces is one of important factors, influencing the distribution of the components between a solution and a solid phase. Adsorption results in accumulation of components from unsaturated solutions on the mineral surfaces, that can be determining at formation a number of ore deposits as well as for the environmental problems, in particular, in an estimation and forecast of reliability of radioactive waste burial (Hochella and White, 1990; Stumm and Morgan, 1987; Stumm, 1992).
To the most dangerous radioactive substances belongs 90Sr formed in nuclear reactions of the uranium fission. Alongside with long half-life (28 years), it has a property to be strongly kept in the living organisms, mainly in the bones, and to be slowly removed, being a source of permanent radiation of a marrow (Korpusov and Oziraner, 1961).
Hematite is a mineral with a well-determined stable surface. The surface properties of hematite are well characterized (Barron and Torrent, 1996; Fokkink, 1989). Its surface structure is close to that of iron hydroxides forming by erosion of base and ultra-base rocks and often controlling contaminant sorption in the subsurface environment.
Review of the literature has shown that the experimental studies of Sr adsorption are scarce. It can be likely explained by quite high pH values of the Sr adsorption edge. There are a few studies (Kinniburgh et al., 1975; Kurbatov et al., 1945; Egorov et al., 1961), the results of which, after Dzombak and Morel, 1989 we do not take into consideration for some reason or other. Mainly, there was no CO2 exclusion during the experiments. Moreover, the method of solid/liquid separation (settling for some hours) is probably not adequate.
In the well known experimental work by Kolarik, 1961 a mutual exchange of Sr2+ ions and protons was studied depending on pH and total Sr concentration. Kolarik considers Sr adsorption as a special case of the complex formation. Despite in this study was also no CO2 exclusion, Dzombak and Morel (1989) could describe the experimental data by Kolarik with the aid of the so called "Two Sites Generalized Two Layer Surface Complexation Theory". As a result of treatment of the experimental data, they obtained a model consisting of three types of surface complexes.
There is another work devoted to Sr reaction and diffusion within iron oxides (Axe and Anderson, 1995). In this work, a significant Sr adsorption (up to 60%) was observed already at pH 5. However, these results are so much unbelievable, that one permits to assume an artefact.
In these works is described only one feature of the Sr adsorption behaviour, namely, adsorption degree depending on pH. However, since proton and hydroxyl-ion are the potential-determining ions for the metal (hydr)oxides, as a basis of any adsorption model has to be a description of acid-base properties. Therfore, as a precondition of independent determination of the model parameters is to be a unique set of the experimental data on adsorption of proton and strontium.
Temperature is one of the major factors influencing the extent of adsorption. In natural aquatic systems (soil and ground waters) adsorption is of importance over a wide temperature range [Hochella and White, 1990). Particularly, it is the case in radioactive waste burial.
The aim of the present work was creation of a thermodynamic model for the heterophaseous system hematite ( FeOH) — H+ — Sr2+ depending on p[H+] and sorbate/sorbent (Sr2+/
FeOH) — H+ — Sr2+ depending on p[H+] and sorbate/sorbent (Sr2+/
 FeOH) ratio at 25, 50, and 75oC with the experimental method representing a combination of acid-base potentiometric titrations with metal adsorption data.
FeOH) ratio at 25, 50, and 75oC with the experimental method representing a combination of acid-base potentiometric titrations with metal adsorption data.
There is no single opinion on the mechanism of Sr adsorption onto oxides.
Adsorption of Sr(II) to goethite was studied by EXAFS spectroscopy (Collins et al., 1996). This qualitative method permits an in situ determination of the immediate coordination sphere around a target metal atom. The results have been interpreted as an existence of both outer-sphere and inner-sphere Sr coordination depending on pH value.
On the other hand, Cowan et al., 1991 modelled a competitive adsorption of Cd and Sr and found that these metals adsorb within the same plane and compete for mutually accessible surface sites by means of mass action. Since Cd is usually considered as a typical specifically adsorbed metal, there is no fundamental difference between the adsorption mechanisms in both cases.
Therefore, it needs to have some tools which could help to distinguish between specifically and non-specifically adsorbed strontium atoms. Thus, in the evaluation of the experimental data the Extended Constant Capacitance Model (ECCM) (Nilsson, 1995) has been used. This model allows us to distinguish between strontium atoms adsorbed at different distances from the surface.
Materials
Hematite (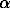 -Fe2O3) (iron(III) oxide of highest grade purity Fe2O3) (REACHIM) was used. The hematite represented a powder consisting of rhombohedric crystalline particles with the average size 5-20
-Fe2O3) (iron(III) oxide of highest grade purity Fe2O3) (REACHIM) was used. The hematite represented a powder consisting of rhombohedric crystalline particles with the average size 5-20 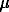 m as well as the fine (< 1
m as well as the fine (< 1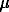 m) fraction. Hematite powder was washed several times with 0.1 M NaCl. Washing was continued until pH became constant.
m) fraction. Hematite powder was washed several times with 0.1 M NaCl. Washing was continued until pH became constant.
The specific surface area was determined by the BET Kr adsorption method to be 6.0 m2 g-1. Hematite structure was confirmed using X-ray diffraction.
Diluted HCl and NaOH solutions were prepared and standardized as described earlier (Karasyova et al., 1998). Solutions of SrCl2 were prepared by dissolving weighed amounts of SrCl2 ·
6H2O (BDH Chemicals p.a.). All solutions were prepared using bidistilled and boiled water.
Methods
The present work was performed as series of acid-base potentiometric titrations at 25.0, 50.0, and 75.0 ±0.2oC. The potentiometric cell, titration procedures, calibration and assumption concerning the glass electrode were previously described Nilsson, 1995, Karasyova et al., 1998. All experiments including calibration of the glass electrode were carried out at constant ionic strength, 0.1 M NaCl. Therefore, we use the notation p[H+] (= -log [H+]), rather than pH.
Before each experiment the total concentration of surface hydroxyl groups was determined by titration of suspension with dilute HCl in the region 2.7 < p[H+] < 3.0. It was 2.5 surface hydroxyl groups / nm2. The solid concentration in all experiments was 70 g dm-3. An aliquote of the Sr(II) solution was then added, and the titration continued by diluted NaOH to p[H+] = 10.0 - 10.2. In several titration points, aliquots of the suspension were sampled, and being protecting from the air, then centrifuged. The total concentration of strontium in the aqueous phase was determined by atomic absorption (AAS (Karl Zeiss)).
Data treatment
In the present investigation, the adsorption equilibria are considered as complexation reactions of strontium with surface hydroxyl groups (
 FeOH) which are formed on the mineral surface during its contact with the aqueous solution. These surface groups can adsorb protons (or hydroxyl-ions) as well as take part in the complexation with metal ions and ligands.
FeOH) which are formed on the mineral surface during its contact with the aqueous solution. These surface groups can adsorb protons (or hydroxyl-ions) as well as take part in the complexation with metal ions and ligands.
One should bear in mind that a notation  FeOH is an obvious simplification of the surface structure, on which there are oxygen atoms with the different coordination. However, this relatively simple model is often satisfactory in the modeling of adsorption data.
FeOH is an obvious simplification of the surface structure, on which there are oxygen atoms with the different coordination. However, this relatively simple model is often satisfactory in the modeling of adsorption data.
Strontium adsorption can be presented as one or several reactions with the surface groups:
 FeOH + Sr2+ <=>
FeOH + Sr2+ <=>  FeOHSr2+ ,
FeOHSr2+ ,
 FeOH + Sr2+ <=>
FeOH + Sr2+ <=>  FeOSr+ + H+ ,
FeOSr+ + H+ ,
 FeOH + Sr2+ + H2O <=>
FeOH + Sr2+ + H2O <=>  FeOSrOH + 2H+ ,
FeOSrOH + 2H+ ,
2( FeOH) + Sr2+ <=> (
FeOH) + Sr2+ <=> ( FeO)2Sr + 2H+ etc.
FeO)2Sr + 2H+ etc.
Since the present work is performed at a constant ionic strength of 0.1 M, to describe the outer-sphere surface complexation of Sr2+ we applied the extended constant capacitance model (ECCM) instead of the triple layer model. This approach is similar to that employed in complexation studies in solution, i.e., outer-sphere complexation of medium ions are not specifically expressed in the equilibrium model. It should be noted that constants evaluated with ECCM are conditional with effects caused by the outer-sphere complexation of medium ions included in the constants.
The surface complexation equilibria in the system  FeOH - H+ - Sr2+ can be written as follows:
FeOH - H+ - Sr2+ can be written as follows:
p H+ + q  FeOH + r Sr2+ <=>
Hp(
FeOH + r Sr2+ <=>
Hp( FeOH)qSrr(p+2r) ;
FeOH)qSrr(p+2r) ;
 inp,q,r (1)
inp,q,r (1)
for inner-sphere complexation and
p H+ + q  FeOH + r Sr2+ <=>
(Ht(
FeOH + r Sr2+ <=>
(Ht( FeOH)qt
Hp-t Srr(p-t+2r) ;
FeOH)qt
Hp-t Srr(p-t+2r) ;  outp,q,r (2)
outp,q,r (2)
for outer-sphere complexation.
The constant for the aqueous equlibrium at 25oC,
Sr2+ + H2O <=>
SrOH+ + H+
which was included in the calculations, was taken from literature and calculated to 50, and 75oC for 0.1 M ionic strength.
The apparent equilibrium constants for the surface complexation reactions,  inp,q,r and
inp,q,r and  outp,q,r as defined by the equations (1), (2), and (3) have been corrected for the coulombic energy of the charged surface to obtain corresponding intrinsic constants:
outp,q,r as defined by the equations (1), (2), and (3) have been corrected for the coulombic energy of the charged surface to obtain corresponding intrinsic constants:
 inp,q,r (int) =
inp,q,r (int) =  inp,q,r e((p+2r)F
inp,q,r e((p+2r)F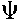 (0)/RT) , (3)
(0)/RT) , (3)
 outp,q,r (int) =
outp,q,r (int) =  outp,q,r e(tF
outp,q,r e(tF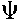 (0)/RT) e((p-t+2r)F
(0)/RT) e((p-t+2r)F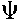 (
( )/RT) (4)
)/RT) (4)
where 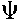 (0) is the electrostatic surface potential at the surface plane and
(0) is the electrostatic surface potential at the surface plane and 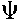 (
( ) the potential at the
) the potential at the  -plane (for weakly bound ions).
-plane (for weakly bound ions).
This extended constant capacitance model (Nilsson,1995) can be regarded as a triple layer model without any diffuse layer. For the potentials and the charges,  o and
o and 
 , at the surface and the
, at the surface and the  -plane the following equations are valid (Nilsson,1995):
-plane the following equations are valid (Nilsson,1995):
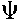 (
( ) = (
) = ( o +
o +

 ) / C2
) / C2
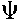 (0) -
(0) - 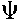 (
( ) =
) =  o / C1 ,
o / C1 ,
where C1 and C2 are the inner and outer layer capacitances, correspondingly.
The total capacitance between the surface and the bulk solution is:
1 / Ctot = 1 / C1 + 1 / C2 . (5)
Optimization of model parameters was performed via the nonlinear least square optimization program FITEQL 3.1 (Herbelin and Westall, 1994). The input of experimental adsorption data into FITEQL was done as described in (Herbelin and Westall, 1994) using a dummy component, Srads. The experimentally determined concentration of adsorbed Sr (difference between the total concentration of Sr and the analyzed Sr concentration in the solution) was equal to the total concentration of the dummy component Srads. The input format for the triple layer model was used, but the ionic strength was set to 109 M in order to reduce the diffuse layer into a plane, as it is assumed in the model. The main indicator of goodness of fit is the overall variance V(Y) which is the weighted sum of squares error divided by the degrees of freedom. Values of V(Y) between 0.1 and 20 indicate a reasonable good fit (Herbelin and Westall, 1994).
The "best" model was obtained by systematic variation of the stoichiometric coefficients p, t, q, and r, searching for the combinations with the lowest value of (Y).
The distribution diagrams have also been calculated with the aid of the FITEQL program.
Experimental potentiometric data can be visualized as Z = f (p[H+]) curves. Z is the average number of protons reacted per  FeOH.
FeOH.
Results and discussion
The System Hematite ( FeOH) — H+
FeOH) — H+
For each titration the total concentration of proton binding sites, B, was determined at 25, 50, and 75oC. The excess of protons was evaluated from data in the range 2.7 < -log[H+] < 3.0 (Karasyova et al., 1998). The value of B in the suspension was found to be 2.0 mM independent on temperature. It corresponds to a surface concentration of 2.85 surface sites/nm2. Thus, a temperature dependence of the site density was not observed.
The evaluation of the acid — base properties of the hematite — solution interface was based on 65 experimental points from 9 experiments. These data were used for evaluation of the protonation and deprotonation constants:
 FeOH + H+ <=>
FeOH + H+ <=>  FeOH2+ ;
FeOH2+ ;
 1,1,0 (6)
1,1,0 (6)
 FeOH <=>
FeOH <=>  FeO- + H+ ;
FeO- + H+ ;
 -1,1,0 . (7)
-1,1,0 . (7)
Details from the data treatment are given in Table 1.
Table 1. Results from evaluation of acid — base properties of hematite surface — solution interface (I = 0.1 M, site density: 2.5 surface hydroxyl groups/nm2).
| T,oC
|
-log[H+], range
|
log  1,1,0 1,1,0
|
log  -1,1,0 -1,1,0
|
Specific capacitance, F m-2
|
V(Y)
|
|
25
|
2.7 - 8.5
|
7.48
|
-9.53
|
1.22
|
8
|
|
8.5 - 10.2
|
7.39
|
-9.59
|
2.49
|
6
|
|
2.7 - 10.2
|
8.05
|
-8.68
|
1.10
|
34
|
|
50
|
2.7 - 8.1
|
7.30
|
-8.91
|
1.00
|
5
|
|
8.1 - 10.2
|
7.28
|
-8.94
|
1.62
|
4
|
|
2.7 - 10.2
|
7.77
|
-8.40
|
0.92
|
29
|
|
75
|
2.7 - 7.8
|
7.45
|
-8.10
|
0.83
|
10
|
|
7.8 - 10.0
|
7.37
|
-8.23
|
1.44
|
3
|
|
2.7 - 10.0
|
7.38
|
-8.02
|
0.88
|
25
|
When we made an attempt to evaluate proton adsorption data from the whole p[H+] range (2.7 to 10.2), overall variance V(Y) was considerable higher (34). An evaluation of experimental data in p[H+] ranges (2.7 to 8.4) and (8.4 to 10.2) separately, that is on different sides of the point of zero charge (point of zero proton condition) resulted in completely acceptable results (Table 1). Moreover, since Sr adsorption takes place at p[H+] higher than the point of zero proton condition, in a treatment of Sr adsorption data we use the acid-base model from alkaline p[H+] range.
Comparing the results obtained for the two p[H+] regions, it is clearly noticeable that the values of specific capacitance differ about two times despite the constants are very similar. This is a common result when applying the Constant Capacitance Model for data evaluation in a wide pH range. For instance, a similar result has been obtained by Schindler and Gamsjäger (1972) who studied acid-base properties of TiO2. They have determined the specific capacitance on alkaline side two times higher than that on acidic side. This surface charge asymmetry may result when there is a difference between the thickness of the double layer formed by different ions: by anions (e.g. Cl-) on acidic side and by cations (e.g. Na+) on alkaline side of the titration curve. Previous studies noted that Na+ screens surface charge more effectively than Cl- (Davis et al., 1978). In the Triple Layer Model this behavior can be described by the different surface complexation strengths of medium ions (Davis et al., 1978, Yates et al., 1974).
In order to evaluate the temperature dependence of proton and hydroxyl-ion adsorption, we combine reactions (6) and (7) deriving the following overall reaction:
 FeOH2+ <=>
FeOH2+ <=>  FeO- + 2H+ ;
FeO- + 2H+ ;
 -11,1,0
-11,1,0  -1,1,0 (8)
-1,1,0 (8)
with
pHpzc = 0.5 (log  1,1,0 - log
1,1,0 - log  -1,1,0) , (9)
-1,1,0) , (9)
where pHpzc is pH of point of zero charge assuming no specific adsorption.
In order to extrapolate pHpzc to 50 and 75oC, we need instead of (9) an isocoulombic (or "balanced-like-charge") reaction, which can be obtained by combining of the dissociation equilibrium of water with a given ionization reaction (Machesky et al., 1994, Schoonen, 1994). This extrapolation is simplified because the significant changes in partial molar heat capacities and volumes are cancelled.
An isocoulombic reaction can be written as follows:
 FeOH2+ + OH- <=>
FeOH2+ + OH- <=>  FeO- + H+ + H2O K1 , (10)
FeO- + H+ + H2O K1 , (10)
log K1 = pKw - 2pHpzc (11)
For our hematite - water interface up to 75oC this difference is approximately constant (log K1 = -3.16±
0.04). An approximate constancy has also been obtained for many oxides and hydroxides (Machesky et al., 1994, 1998, Tewari and Campbell, 1976, Ivanova and Lakshtanov, 1994). Indeed, one can see in Table 1 that the proton adsorption ( 1,1,0) is practically independent on temperature as the temperature dependence of 1/2 log
1,1,0) is practically independent on temperature as the temperature dependence of 1/2 log  -1,1,0 is equidistant to that of 1/2 pKw. This means, that proton adsorption, i.e. reaction with the surface OH-groups, is a process similar to its reaction with hydroxyl-ion in the solution.
-1,1,0 is equidistant to that of 1/2 pKw. This means, that proton adsorption, i.e. reaction with the surface OH-groups, is a process similar to its reaction with hydroxyl-ion in the solution.
The System Hematite ( FeOH) — H+ — Sr2+
FeOH) — H+ — Sr2+
Strontium adsorption was studied in 5 titrations in the range 6 < p[H+] < 10.2. The ratios in total concentrations of Sr(II) and (FeOH were 0.1, 0.5, and 1.0. In order to illustrate the results of the potentiometric titrations, the average number of protons reacted per  FeOH, Z versus p[H+] , are plotted in Fig.1, 2, and 3.
FeOH, Z versus p[H+] , are plotted in Fig.1, 2, and 3.
Fig.1.
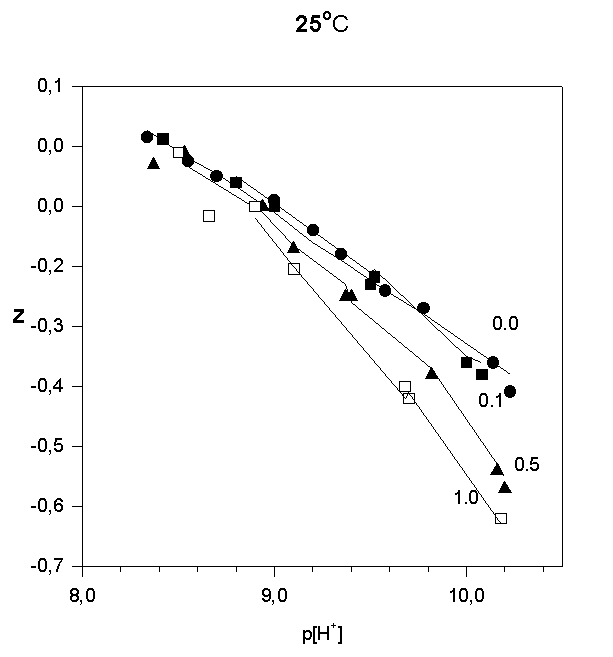
Fig.2.
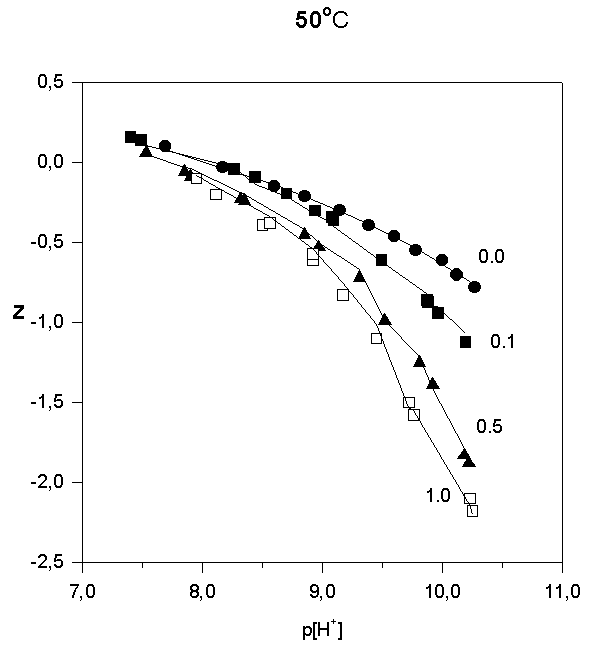
Fig.3.
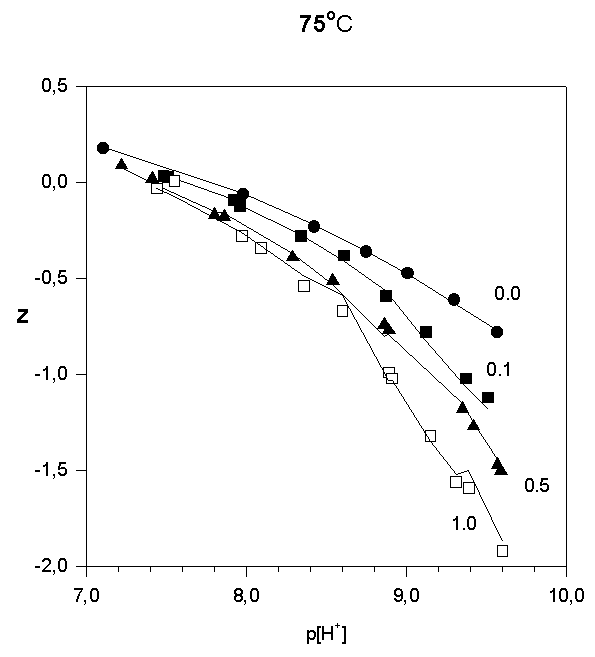
The adsorption data are shown in Fig.4,5,and 6.
Fig.4.
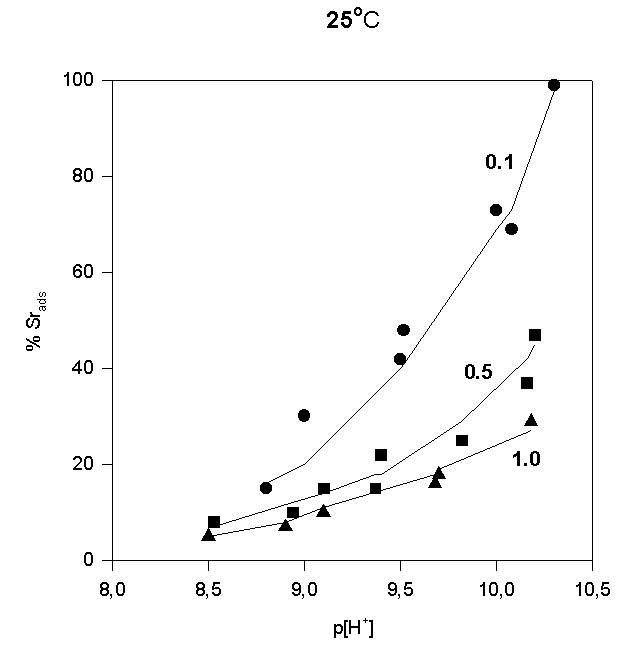
Fig.5.
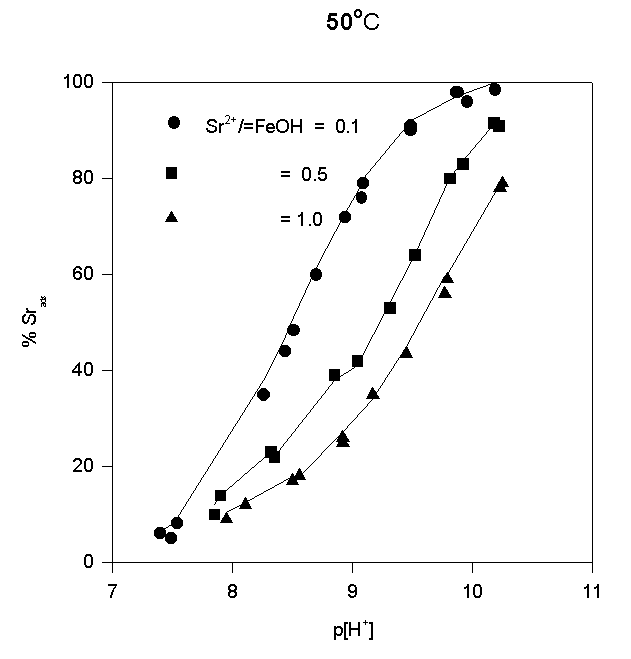
Fig.6.
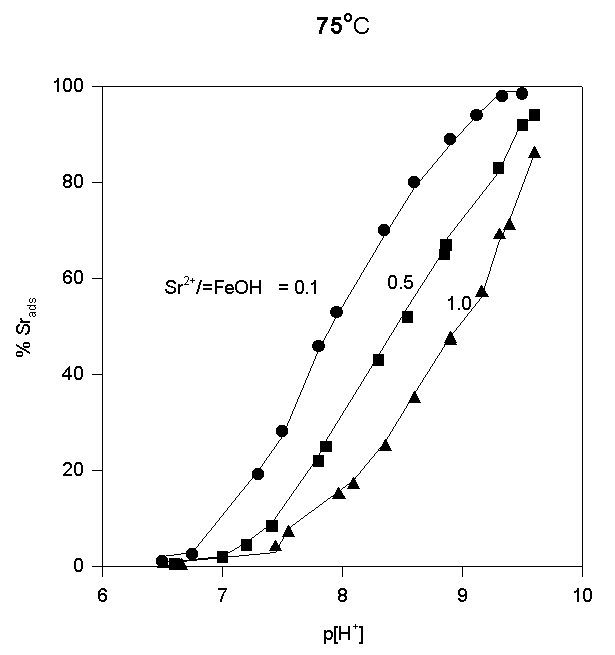
Like most cations, adsorption of strontium increases with increasing p[H+]. No significant adsorption was observed below p[H+] = 7. As the sorbate to sorbent ratio increases, the adsorption edge shifts to higher p[H+] values. Under the experimental conditions, the adsorption edge covers a wider pH range than for transition metal cations like Pb, Cu, Co, Ni etc. Such a behavior is typical for all alkaline earth cations (Dzombak and Morel, 1990). Their adsorption is also more sensitive to ionic strength and exhibits lower stoichiometry of proton release than that of other cations. These results have been reported in literature for Ca2+ adsorption on. An increase of ionic strength from 0.01 to 0.1 M resulted in a small but detectable decrease in Ca2+ adsorption goethite (Ali and Dzombak, 1996). This reflects the contribution of coulombic forces to the overall change in free energy of the adsorption.
In the case of Sr2+, adsorption at the hematite surface takes place over a p[H+] range where the surface is negatively charged, that is where coulombic forces are attractive. Indeed, in this case a significant electrostatic contribution can be expected, and outer-sphere complexes may be formed as a result.
Thus, there are indications that strontium may form inner-sphere as well as outer-sphere complexes.
Since Sr adsorption occurs mainly in the region above PPZC (8.5), data treatment was based on 20 experimental points with measurements of both soluble Sr(II) and [H+] in the range 8.5 < p[H+] < 10.2, for which we have a reliable acid-base model. The equilibrium constants for the acid-base reactions as well as the surface site density and the value of total capacitance Ctot for the double layer were considered as known parameters and used without modifications (Table 1). The equilibrium constants for the auto protolysis of water at different temperatures (0.1 M ionic strength) were taken from (Baes and Mesmer, 1976).
The evaluation of the model consisted of a test of combinations of complexes with various compositions. Both inner-sphere and outer-sphere as well as monodentate and bridging surface complexes were tested. When combinations with both inner- and outer-sphere complexes tested, we could not reach a minimum of the V(Y) value. It decreased gradually as C1 increased, approaching V(Y) value for a given combination with inner-sphere complexes only. This indicates a collapse of the layer between 0- and  -plane, i.e. Sr adsorbs at the same plane as protons and hydroxyl-ions. Therefore, the Extended CCM based model becomes the same as the ordinary CCM.
-plane, i.e. Sr adsorbs at the same plane as protons and hydroxyl-ions. Therefore, the Extended CCM based model becomes the same as the ordinary CCM.
The details from the data treatment with inner-sphere complexes only are given in Table 2.
Table 2. Results from optimization of stability constants for combinations of surface complexes in the system  FeOH — H+ — Sr2+. V(Y) is the overall variance in errors in the mass balances for H+ and Sr2+. All the complexes are the inner-sphere.
FeOH — H+ — Sr2+. V(Y) is the overall variance in errors in the mass balances for H+ and Sr2+. All the complexes are the inner-sphere.
|
|
|
V(Y)

|
|
N
|
Combination of surface complexes
|
25oC
|
50oC
|
75oC
|
|
1
|
1,2
|
16
1.72; -8.00
|
72
2.50; -6.00
|
100
2.54; -5.18
|
|
2
|
1,3
|
13
1.80; -17.86
|
18
2.85; -15.53
|
25
3.01; -14.16
|
|
3
|
1,4
|
13
1.79; -17.69
|
55
2.77; -15.09
|
83
2.92; -13.68
|
|
4
|
2,3
|
without converg.
|
69
-5.92; -15.95
|
67
-5.19; -14.46
|
|
5
|
2,3,5
|
12
-8.50; -17.72; 1.82
|
19
-6.29; -15.54; 2.77
|
26
-5.80; -14.06; 2.98
|
|
6
|
2,5
|
15
-7.81; 1.72
|
69
-5.91; 2.49
|
97
-5.13; 2.52
|
|
7
|
3,5
|
12
-17.62; 1.86
|
24
-15.29; 2.92
|
28
-13.95; 3.06
|
|
8
|
4,5
|
12
-17.46; 1.84
|
54
-14.90; 2.83
|
79
-13.52; 2.94
|
|
9
|
2,4,5
|
without converg.
|
without converg.
|
without converg.
|
|
10
|
3,4,5
|
12
-18.20; -17.59; 1.84
|
23
-15.31; -15.87; 2.90
|
28
-13.95; -15.01; 3.05
|
1 -  FeOHSr2+; 2 -
FeOHSr2+; 2 -  FeOSr+; 3 -
FeOSr+; 3 -  FeOSrOH;
4 - (
FeOSrOH;
4 - ( FeO)2Sr; 5 - (
FeO)2Sr; 5 - ( FeOH)2Sr2+
FeOH)2Sr2+
Based on the data at 25oC only, we can not choose some appropriate model. Indeed, almost all models listed in Table 2 describe satisfactorily the experimental data. This indicate the V(Y) values which fall within the range of a reasonable good fit (Herbelin and Westall, 1994). However, assuming that surface speciation does not change in the temperature range studied, the V(Y) values at 50 and 75oC allow to choose the adequate models. The best fit could be obtained by a model (N2 in Table 2) consisting of the two surface complexes with the overall stoichiometries, defined according to equation (2), (0, 1, 1) and (-2, 1, 1). These stoichiometries can be interpreted as formation of a series of inner-sphere monodentate complexes according to the following equilibria:
 FeOH + Sr2+ <=>
FeOH + Sr2+ <=>  FeOHSr2+
FeOHSr2+
 in0,1,1 (8)
in0,1,1 (8)
 FeOH + Sr2+ + H2O <=>
FeOH + Sr2+ + H2O <=>  FeOSrOH + 2H+
FeOSrOH + 2H+
 in-2,1,1 . (9)
in-2,1,1 . (9)
A good fit was also obtained with the models (NN 5 and 10 in Table 2) each consisting of three inner-sphere surface complexes with the following stoichiometries:
N5: (0, 2, 1), (-1, 1, 1), (-2, 1, 1)
N10: (0, 2, 1), (-2, 1, 1), (-2, 2, 1).
A formation of surface complexes with these stoichiometries can be described by the following equations:
 FeOH + Sr2+ <=>
FeOH + Sr2+ <=>  FeOSr+ + H+
FeOSr+ + H+
 in-1,1,1 (10)
in-1,1,1 (10)
2 FeOH + Sr2+ <=> (
FeOH + Sr2+ <=> ( FeOH)2Sr2+
FeOH)2Sr2+
 in0,2,1 (11)
in0,2,1 (11)
2 FeOH + Sr2+ <=> (
FeOH + Sr2+ <=> ( FeO)2Sr + 2H+
FeO)2Sr + 2H+
 in-2,2,1 . (12)
in-2,2,1 . (12)
A model similar to N5 (Table 3): (-1, 1, 1), (-2, 1, 1), (0, 2, 1) was obtained by Ali and Dzombak, 1996 from fitting of Ca adsorption data sets using FITEQL. Nevertheless, a formation of the bidentate complexes on the hematite surface should be declined by the following consideration. The Sr atom has eight water molecules in its hydration sphere. It is coordinated to a total 8 oxygen atoms at 2.6 Å
and lies at the center of a cube. Therefore, a distance between O atoms along the edge of a square is 3 Å
. A distance between the reactive OH-groups (Fe-Fe or O-O) is 5.03 Å
, i.e. the surface of hematite appears to be a poor template for the bidentate binding of Sr, as opposed to the goethite surface where the distance between nighboring reactive OH-groups is 3.04 Å
and closely matches the distance between O-atoms in hydration sphere of Sr. Hence, the models with the bidentate surface complexes (NN 5 and 10) were rejected.
Thus, the model we propose here consists of two monodentate surface complexes, as is summarized in Table 3.
Table 3. The proposed model for the surface complexation of Sr on hematite (I = 0.1 M NaCl).
|
T, oC
|
log  0,1,1 0,1,1
|
log  -2,1,1 -2,1,1
|
V(Y)
|
|
Sr + H
data
|
Sr
data only
|
Sr + H
data
|
Sr
data only
|
Sr + H
data
|
Sr
data only
|
Ctot
F m-2
|
Site density
nm-2
|
|
25
|
1.80 ±
0.02
|
1.82 ±
0.05
|
-17.86 ±
0.05
|
-17.88 ±
0.07
|
13
|
16
|
2.49
| 2.85
|
|
50
|
2.84 ±
0.02
|
2.79 ±
0.03
|
-15.53 ±
0.02
|
-15.56 ±
0.03
|
18
|
2
|
1.62
|
|
75
|
3.01 ±
0.02
|
2.96 ±
0.03
|
-14.15 ±
0.02
|
-14.15 ±
0.03
|
27
|
13
|
1.44
|
Formation constants given in Table 3 increase between 25 and 75oC. These temperature-dependent constants and the van't Hoff equation below can be used to evaluate reaction enthalpy and entropy for reactions (8) and (9):
log  =
=  H/2.3RT +
H/2.3RT +  S/2.3R , (13)
S/2.3R , (13)
where  H and
H and  S are the enthalpy and entropy of reaction correspondingly, R is the gas constant, T is the absolute temperature. Provided enthalpy and entropy are constant in the temperature range studied, a plot of log
S are the enthalpy and entropy of reaction correspondingly, R is the gas constant, T is the absolute temperature. Provided enthalpy and entropy are constant in the temperature range studied, a plot of log  versus 1/T results in a straight line with slope
versus 1/T results in a straight line with slope
 H/2.3R and intercept
H/2.3R and intercept  S/2.3R. It should be noted that the reactions (8) and (9) are not isocoulombic reactions and the assumption of the constancy of
S/2.3R. It should be noted that the reactions (8) and (9) are not isocoulombic reactions and the assumption of the constancy of  H and
H and  S is not strong. However, we assumed that in this quite narrow temperature range
S is not strong. However, we assumed that in this quite narrow temperature range
 Cp = 0, and the van't Hoff equation (13) can be used for the determination
Cp = 0, and the van't Hoff equation (13) can be used for the determination  H and
H and  S. Table 4 contains the enthalpy and entropy changes for adsorption of Sr(II) obtained from the surface complexation constants given in Table 4. All enthalpy values testify that the adsorption reactions are endothermic.
S. Table 4 contains the enthalpy and entropy changes for adsorption of Sr(II) obtained from the surface complexation constants given in Table 4. All enthalpy values testify that the adsorption reactions are endothermic.
Table 4. Thermodynamic parameters for surface reactions
|
Surface reaction
|
 H H
(kJ/mole)
|
 S S
(J / K mole)
|
 FeOH + Sr2+ <=> FeOH + Sr2+ <=>  FeOHSr2+ FeOHSr2+
|
48 ± 2
|
196 ± 5
|
 FeOH + Sr2+ + H2O <=> FeOH + Sr2+ + H2O <=>  FeOSrOH + 2H+ FeOSrOH + 2H+
|
147 ±3
|
153 ±9
|
Strontium adsorption enthalpies are 48 and 147 kJ/mole for  FeOHSr2+ and
FeOHSr2+ and  FeOSrOH respectively. There is a big difference between the formation enthalpies of these surface complexes. This may indicate the different energetics of Sr adsorption in the different p[H+] regions, i.e. outer- or inner-sphere complexes may be formed. In the EXAFS work by Collins et al., (1996), samples of Sr(II) adsorbed on goethite were examined at pH 9.2 and 10.2. For the sample at pH 9.2 outer-sphere coordination was inferred since no neighbour Fe atoms were found. In contrast, at pH 10.2 a second shell of two Fe atoms at 4.3 Å was also revealed. This distance is consistent with the formation of an inner-sphere complex where Sr binds to oxygen atom of two adjacent Fe atoms in the goethite lattice.
FeOSrOH respectively. There is a big difference between the formation enthalpies of these surface complexes. This may indicate the different energetics of Sr adsorption in the different p[H+] regions, i.e. outer- or inner-sphere complexes may be formed. In the EXAFS work by Collins et al., (1996), samples of Sr(II) adsorbed on goethite were examined at pH 9.2 and 10.2. For the sample at pH 9.2 outer-sphere coordination was inferred since no neighbour Fe atoms were found. In contrast, at pH 10.2 a second shell of two Fe atoms at 4.3 Å was also revealed. This distance is consistent with the formation of an inner-sphere complex where Sr binds to oxygen atom of two adjacent Fe atoms in the goethite lattice.
However, the enthalpy for the surface complex  FeOHSr2+ falls within the range of parameters calculated for adsorption of heavy metals for which this great energy input is needed for the partial dehydration of the metal ions during the formation of inner-sphere complexes. Figure 7 shows the temperature dependence of the formation constants for all complexes appearing in the models listed in Table 2.
FeOHSr2+ falls within the range of parameters calculated for adsorption of heavy metals for which this great energy input is needed for the partial dehydration of the metal ions during the formation of inner-sphere complexes. Figure 7 shows the temperature dependence of the formation constants for all complexes appearing in the models listed in Table 2.
Fig.7.
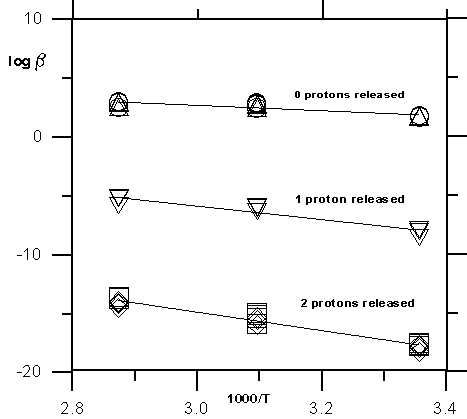
It can be seen a regular increase of the line slopes with the number of protons released during adsorption. The enthalpy value estimated for the surface complex  FeOSrOH is much larger because its formation always includes coadsorption of two hydroxide-ions (or desorption of two protons). Indeed, from the data in Table 1, enthalpy of OH- adsorption is calculated to be 54 kJ/mole. The sum of the enthalpies of Sr attachment to the surface (reaction 8) and OH- adsorption (reaction 7) (102 kJ/mole) should give the formation enthalpy of surface complex
FeOSrOH is much larger because its formation always includes coadsorption of two hydroxide-ions (or desorption of two protons). Indeed, from the data in Table 1, enthalpy of OH- adsorption is calculated to be 54 kJ/mole. The sum of the enthalpies of Sr attachment to the surface (reaction 8) and OH- adsorption (reaction 7) (102 kJ/mole) should give the formation enthalpy of surface complex  FeOSr+ to which the middle line in Fig. 7 with one proton released corresponds (109 kJ/mole). The same value should be added to the last one to obtain the entalpy of the surface complex
FeOSr+ to which the middle line in Fig. 7 with one proton released corresponds (109 kJ/mole). The same value should be added to the last one to obtain the entalpy of the surface complex  FeOSrOH with two protons released. As a result we obtain the value 156 kJ/mole that is very close to
FeOSrOH with two protons released. As a result we obtain the value 156 kJ/mole that is very close to
 H = 147 kJ/mole from Table 4. It should be noted however that it is an approximate estimation because we use the entalpy of hydroxide-ion adsorption to the uncharged surface (reaction 8) whereas the follow reactions should be considered:
H = 147 kJ/mole from Table 4. It should be noted however that it is an approximate estimation because we use the entalpy of hydroxide-ion adsorption to the uncharged surface (reaction 8) whereas the follow reactions should be considered:
 FeOHSr2+ + OH- =
FeOHSr2+ + OH- =  FeOSr+ and
FeOSr+ and
 FeOSr+ + OH- =
FeOSr+ + OH- =  FeOSrOH .
FeOSrOH .
Therfore, the value of 156 kJ/mole is probably overestimated.
Thus, the enthalpy of the single Sr attachment to the surface hydroxyl groups (48 kJ/mole) corresponds to the values typical for the formation of inner-sphere surface complexes. Moreover, this confirms the entropy value of 196 J / K mole which is to be related to the dehydration of Sr(II). The literature value for the entropy of hydration of Sr2+ ions in aqueous solutions amounts to -205 J / K mole (Burgess, 1978). It can be inferred that nearly the whole hydration entropy was gained when Sr adsorbs. This also confirms a conclusion obtained from the fitting of experimental data that strontium adsorbs onto the hematite surface in a similar manner independent on pH.
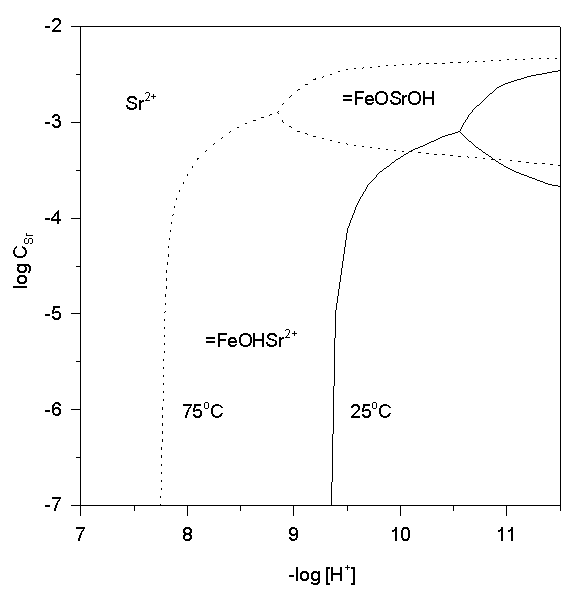
The combined effect of the pHpzc decrease and the positive enthalpies of surface complexes formation is to favor strontium adsorption at hematite surface at enhanced temperatures. Strontium adsorption and retardation in the natural aquatic environment is unlikely at ambient T and pH, but may be significant in the radioactive waste disposal at elevated temperatures. The predominance area diagram (Fig. 8) show that p[H+] of Sr adsorption decreases by 1.6 units as temperature rises from 25 to 75oC.
Fig.8.
Acknowledgments
Valuable discussions with Staffan Sjöberg on mechanisms of strontium adsorption are gratefully acknowledged. We also thank Agneta Nordin for help and advice. This work was funded by the Russian Foundation for Basic Research, grant N97-05-65738.
References
- Ali M.A. and Dzombak D.A. (1996) Effects of simple organic acids on sorption of Cu2+ and Ca2+ on goethite. Geochim. Cosmochim. Acta 60, 291-304.
- Axe L. and Anderson P.R. (1995) Sr diffusion and reaction within Fe oxides: evaluation of the rate-limiting mechanism for sorption. J. Coll. Int. Sci. 175, 157-165.
- Baes C.F., Jr and Mesmer R.E. (1976) The Hydrolysis of Cations. J. Wiley & Sons.
- Barron V. and Torrent J. (1996) Surface hydroxyl configuration of various crystal faces of hematite and goethite. J. Coll. Int. Sci. 177, 407-410.
- Burgess J. (1978) Metal ions in solution. Ellis Horwood Ltd., Chichester.
- Collins C.R., Sherman D.M., and Ragnarsdottir K.V. (1996) Adsorption of Hg(II) and Sr(II) to goethite studied by EXAFS spectroscopy. Abstracts of Research Conference on Geochemistry of Crustal Fluids: Water/rock interaction during natural processes, Seefeld,, 37.
- Cowan C.E., Zachara J.M., and Resch C.T. (1991) Cadmium adsorption on iron Oxides in the presence of alkaline-earth elements. Environ. Sci. Technol. 25, 437-446.
- Davis J.A., James R.O., and Leckie J.O. (1978) Surface ionization and complexation at the oxide/water interface. 1.Computation of electrical double layer properties in simple electrolytes. J. Colloid Interface Sci., 63, 480-499.
- Dzombak D.A. and Morel F.M.M. (1990) Surface complexation modeling. Hydrous ferric oxide. J.Wiley & Sons. NY.
- Fokkink L.G.J. (1987) Ion adsorption on oxides. Ph.D.dissertation, Univ. Wageningen, Wageningen.
- Fokkink L.G.J., De Keizer A., and Lyklema J. (1989) Temperature dependence of the electrical double layer on oxides: rutile and hematite. J. Coll. Int. Sci. 127, 116-131.
- Egorov Y.V., Pushkarev V.V., and Tkachenko E.V. (1961) Coprecipitation of strontium with ferric hydroxide and active manganese dioxide from aqueous solutions. Russ. J. Inorg. Chem. 6, 256-258.
- Herbelin A.L., and Westall J.C. (1994) FITEQL: A computer program for determination of chemical equilibrium constants from experimental data. Version 3.1. Report 94-01. Dept. of Chemistry, Oregon State Univ. Corvallis, OR, USA.
- Hiemstra T., De Wit J.C.M., and Riemsdijk W.H.V. (1989) Multisite proton adsorption modeling at the solid/solution interface of (hydr)oxides: A new approach. II. Applications to various important (hydr)oxides. J. Coll. Int. Sci. 133, 105-117.
- Hochella M.F. and White A.F. (1990) Mineral-water interface geochemistry: An overview. In Mineral-Water Interface Geochemistry (ed. M.F.Hochella and A.F.White); Rev. Mineral. 23, Chap. 1.
- Karasyova O.N., Ivanova L.I., Lakshtanov L.Z., Lövgren L., and Sjöberg S. (1998) Complexation of gold(III)-chloride at the surface of hematite. Aquatic geochemistry,
- Ivanova L.I. and Lakshtanov L.Z. (1994) Surface properties of aluminium and silicon oxides in electrolyte solutions at temperatures up to 250oC. In: Experimental problems of geology. Zharikov V.A. ed. Nauka, Moscow. 578-588.
- Kinniburgh D.G., Syers J.K., and Jackson M.L. (1975) Specific adsorption of trace amounts of calcium and strontium by hydrous oxides of iron and aluminium. Soil Sci. Soc. Am. J. 39, 464-470.
- Kolarik Z. (1961) Sorption radioaktiver Isotopen an Niederschlagen. VI. Systeme Eisen(III)-Hydroxyd-Strontiumnitratlösung und die allgemeinen gesetzmässigkeiten der Sorption am Eisen(III)-Hydroxyd. Collection Czech. Chem. Commun. 27, 938-949.
- Korpusov G.V. and Oziraner S. (1961) Radioactive strontium. Gosatomizdat.
- Kurbatov M.H., Kulp J.L., and Mack E. (1945) Adsorption of strontium and barium ions and their exchange on hydrous ferric oxide. J. Am. Chem. Soc. 67, 1923-1929.
- Machesky M.L., Palmer D.A., and Wesolowski D.J. (1994) Hydrogen ion adsorption at the rutile-water interface to 250oC. Geochim. Cosmochim. Acta 58, 5627-5632.
- Machesky M.L., Wesolowski D.J., Palmer D.A., and Ichiro-Hayashi K. (1998) Potentiometric titrations of rutile suspensions to 250oC. J. Colloid Interface Sci. 200, 298-309.
- Nilsson N. (1995) Inner/outer sphere complexation of phosphate and organic ligands at the goethite-water interface. Ph.D.Dissertation, Umea univ.
- Schindler P.W., and Gamsjäger H. (1972) Acid-base reactions of the TiO2 (anatase) – water interface and the zero point of charge of TiO2 suspensions. Kolloid-Z u. Z. Polymere 250, 759-765.
- Schoonen M.A.A. (1994) Calculation of the point of zero charge of metal oxides between 0 and 350oC. Geochim. Cosmochim. Acta 58, 2845-2851.
- Stumm W. and Morgan J.J. (1987) Aquatic geochemistry. 2nd ed. J.Wiley & Sons, NY.
- Stumm W. (1992) Chemistry of the solid-water interface. J.Wiley & Sons, NY.
- Tewari P.H. and Campbell A.B.(1976) ) Temperature dependence of point of zero charge of cobalt and nickel oxides and hydroxides. J. Colloid Interface Sci. 55, 591-600.
- Yates D.E., Levine S., and Healy T.W. (1974) Site-binding model of the electrical double layer at the oxide-water interface. J. Chem. Soc. Faraday Trans. 1, 70, 1807-1818.
 -Fe2O3) (iron(III) oxide of highest grade purity Fe2O3) (REACHIM) was used. The hematite represented a powder consisting of rhombohedric crystalline particles with the average size 5-20
-Fe2O3) (iron(III) oxide of highest grade purity Fe2O3) (REACHIM) was used. The hematite represented a powder consisting of rhombohedric crystalline particles with the average size 5-20 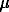 m as well as the fine (< 1
m as well as the fine (< 1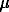 m) fraction. Hematite powder was washed several times with 0.1 M NaCl. Washing was continued until pH became constant.
m) fraction. Hematite powder was washed several times with 0.1 M NaCl. Washing was continued until pH became constant.
 FeOH) — H+ — Sr2+ depending on p[H+] and sorbate/sorbent (Sr2+/
FeOH) — H+ — Sr2+ depending on p[H+] and sorbate/sorbent (Sr2+/
 inp,q,r (1)
inp,q,r (1)
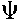 (0)/RT) , (3)
(0)/RT) , (3)
 o and
o and 





 H/2.3RT +
H/2.3RT + 
